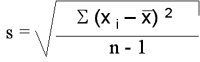|
Seis Sigma Variação - A raiz de todos os males i Six Sigma Como cliente, a pior experiência que eu poderia imaginar é ser vítima da variação de um processo. "Não parece ser tão ruim assim", você pode estar pensando. Procure se lembrar da última vez em que você:
É provável que você consiga fazer uma pequena lista de suas próprias experiências ruins sem fazer muito esforço, mas é provável que você se lembre também de quando pegou a fila mais rápida no supermercado, recebeu um corte de cabelo perfeito e ficou pasmo com o conhecimento do vendedor que o atendeu. Foi uma sensação ótima, não foi? Vamos examinar algumas maneiras que podem nos ajudar a avaliar a variação em processos. Primeiramente, é importante entrar no espírito da coisa - imagine que seus filhos tenham passado o dia todo implorando por uma pizza e, no caminho para casa, você pára para pedir uma pizza pela qual você ficará aguardando no local. Analise o conceito de variação examinando o tempo de preparação (em minutos) de 10 pizzas feitas por duas pizzarias concorrentes. Veja abaixo a lista de tempos.
Se usarmos ferramentas estatísticas comuns, como média, mediana, moda e amplitude média, obtemos os seguintes resultados:
A partir desses resultados, podemos perceber que as duas pizzarias têm as mesmas medidas de tendência central; assim, em média, os clientes esperam a mesma quantidade de tempo pelas pizzas nos dois restaurantes. Baseando-se apenas nessas medidas, não é possível perceber qualquer diferença entre os dois processos. Contudo, se voltarmos aos dados originais, perceberemos uma diferença bastante distinta: o tempo de preparação da Pizzaria ABC varia muito menos do que o tempo da Pizzaria XYZ. Se todas as outras características da pizza (sabor, temperatura, tamanho, recheio, qualidade, cordialidade no atendimento etc) forem iguais, é mais provável que o cliente prefira a Pizzaria ABC, onde não há a possibilidade de ficar aborrecido por ser a única pessoa cujo tempo de preparação da pizza é muito mais lento do que o dos outros. Verificando e comparando as diferenças de variação entre o tempo de preparação das duas empresas, podemos ter uma idéia do que é variação. Porém, nos negócios, é preciso mais do que uma idéia - é preciso medir e quantificar a variação dos processos. Por essa razão, apresentaremos a seguir o uso de duas ferramentas: amplitude e desvio-padrão. Usando a Amplitude para Entender a Variação
No caso da Pizzaria ABC, a amplitude é a diferença entre 7,7 minutos (maior valor) e 6,5 minutos (menor valor), que é igual a 1,2 minutos. A amplitude do tempo de preparação da Pizzaria XYZ é: 10,0 - 4,2 = 5,8 minutos. Essa amplitude dos dados, muito maior do que a anterior, sugere que o processo da Pizzaria XYZ apresenta uma quantidade maior de variação associada.
A amplitude, nesse caso, pode induzir a erro, pois utiliza apenas os valores
máximo e mínimo do conjunto de dados. O desvio-padrão seria uma ferramenta
melhor para calcular a variação nesse caso. Usando o Desvio-Padrão para Entender a Variação
Utilizando essa fórmula, agora podemos comparar a variação das duas pizzarias e observar que o desvio-padrão referente à Pizzaria ABC (0,48 minutos) é muito menor do que o desvio-padrão referente à Pizzaria XYZ (1,82 minutos). Isso dá suporte à nossa observação inicial dos dados e aos nossos resultados da amplitude como quantificação da variação. OBS: Em nossa definição de desvio-padrão, referimo-nos ao desvio-padrão de dados de uma amostra como s. Se quiséssemos calcular o desvio-padrão ( s ) de uma população, dividiríamos pelo tamanho da população (N), e não por n-1.
|